Majoritatea oamenilor atunci cand aud de “numere complexe” inteleg de fapt “numere complicate”. Da, vorbesc despre numerele acelea care au o parte reala si o parte imaginara. Acele numere care au aparut pentru ca ecuatii de genul x^2 + 1 = 0 sa aiba si ele solutii. (Prin x^2 notez “x la puterea 2”, sau “x patrat”.)

Ce legatura au numerele complexe cu subiectul acestui articol? O sa vezi imediat…

Dar mai intai: Care este subiectul acestui articol? 🙂

Sa zicem ca ai un robotel (pe care il poti reprezenta in ecranul igotopic folosind un punct albastru) care stie sa raspunda la doar trei comenzi:

(1) mergi un pas in fata

(2) intoarce-te la stanga (90 de grade)

(3) intoarce-te la dreapta (90 de grade).

Inseamna ca robotelul asta poate fi caracterizat la orice moment de timp prin intermediul a doua puncte:

(1) un punct (albastru, sa zicem) ce marcheaza pozitia robotelului pe ecran

(2) si un alt punct (galben, sa zicem), adiacent primului punct si care reprezinta directia de mers a robotelului.

Ca sa iti fie clar la ce ma refer, iata mai jos robotelul nostru in actiune. Il poti comanda folosind tastele: ‘a‘ <– pentru intoarcere la stanga, ‘d‘ <– pentru intoarcere la dreapta si ‘w‘ pentru inaintare cu un pas in directia curenta de mers. (Pentru a porni programul apasa butonul Reseteaza si apoi butonul Executa.)

// ----------------------------------
// Joc robotel stanga-dreapta-inainte
// ----------------------------------

// Datele programului:

var rx = 5;
var ry = 5;

var dx = 0;
var dy = 1;

// Functii ajutatoare:

function StergeEcran()
{
  var i = -1;
  var j;
  while (i<13)
  {
    j = -1;
    while (j<13)
    {
      Stinge(i, j);
      j = j+1;
    }
    i = i+1;
  }
}

function AfiseazaRobotel()
{
  Aprinde(rx, ry, ALBASTRU);
  Aprinde(rx+dx, ry+dy, GALBEN);
}

function FunctieTaste(ev)
{
  var tasta = TastaApasata(ev);
  var tmp;
  if (tasta == 'a')
  {
    tmp = dx;
    dx = -dy;
    dy = tmp;
  }
  else if (tasta == 'd')
  {
    tmp = dx;
    dx = dy;
    dy = -tmp;
  }
  else if (tasta == 'w')
  {
    rx = rx+dx;
    ry = ry+dy;
  }
  StergeEcran();
  AfiseazaRobotel();
}

// Programul propriu-zis:

StergeEcran();
AfiseazaRobotel();
AscultaTaste(FunctieTaste);

E fain robotelul, nu? 🙂

Acum ca te-ai jucat nitel si ai vazut care e ideea, hai sa revenim un pic la munca.

Cum ai face sa schimbi directia de mers a robotelului? Adica, de exemplu, cum ai face ca atunci cand utilizatorul apasa tasta ‘a‘ robotelul sa se intoarca la stanga cu 90 de grade?

Daca ai parcurs constiincios tutorialul de aici ar trebui sa nu iti fie foarte greu sa dai un raspuns la intrebarea de mai sus.

Doar ca cel mai probabil raspunsul tau ar fi ceva de genul:

daca s-a apasat tasta 'a'
{
   daca directia este Nord
      directia devine Vest
   daca directia este Vest
      directia devine Sud
   daca directia este Sud
      directia devine Est
   daca directia este Est
      directia devine Nord
}

^– Nu-i asa ca la ceva de genul asta te-ai fi gandit?

Insa daca te-ai uitat in codul sursa al programului de mai sus ai vazut ca solutia adoptata de mine arata asa:

if (tasta == 'a')
{
   tmp = dx;
   dx = -dy;
   dy = tmp;
}

Ceea ce intr-un limbaj mai omenesc s-ar traduce in:

daca s-a apasat tasta 'a'
{
   noul dx devine -dy
   noul dy devine vechiul dx
}

Uau!! Acelasi efect, dar scriind mult mai putin.

Oare cum e posibil asa ceva? Simplu — cu numere complexe! 🙂

Probabil ai remarcat ca pozitia robotelului pe ecran am memorat-o in variabilele rx si ry, iar pentru directia de mers a robotelului am folosit variabilele dx si dy. Impreuna dx si dy formeaza un versor, adica un vector (dx, dy) al carui modul este 1 si care indica o directie si un sens intr-un spatiu (bidimensional, in cazul nostru). Poate ca afirmatia asta este mai clara daca privesti figura urmatoare:

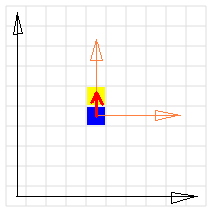
(In figura vectorul (dx, dy) este reprezentat cu linie rosie groasa. Valorile componentelor acestui vector se raporteaza la sistemul de axe portocaliu. (Acest sistem de axe este mobil, avand originea in pozitia curenta a robotelului, ale carei coordonate se raporteaza la sistemul de axe negru.))

Un vector bidimensional seamana mult cu un numar complex. Principala asemanare consta in faptul ca ambele sunt caracterizate de doua marimi (adica, practic, de doua numere). Daca in cazul unui vector bidimensional cele doua marimi sunt componenta pe prima axa a spatiului si, respectiv, componenta pe cea de-a doua axa, in cazul unui numar complex cele doua marimi sunt partea reala si, respectiv, partea imaginara.

Asta inseamna ca putem privi vectorul de directie (dx, dy) ca pe un numar complex dx+i*dy (unde prin i am notat valoarea unitatii de pe axa imaginara (adica i = radical(-1)).

Dar si un numar complex a+i*b poate fi privit ca un vector de modul egal cu radical(a*a+b*b) si unghi egal cu arctan(b/a) (+ pi radiani, daca a<0). Si poate fi notat ca a+i*b = modul * e^(i*unghi).

OK, si ce-i cu asta?

Pai, ce se intampla atunci cand inmultesti doua numere complexe?

Hai sa vedem cat face modul1*e^(i*unghi1) inmultit cu modul2*e^(i*unghi2). Chiar daca matematica de pana aici din acest articol ti-a dat unele batai de cap, banuiesc ca iti dai seama ca rezultatul va fi modul1*modul2*e^(i*unghi1)*e^(i*unghi2) ceea ce e egal cu (modul1*modul2)*e^(i*(unghi1+unghi2)).

Deci, ce s-a intamplat? Am inmulti doua numere complexe, iar rezultatul este un numar complex al carui modul este produsul celor doua module, iar unghiul este suma celor doua unghiuri.

Bun! Si cum putem folosi asta pentru a calcula intoarcerea la stanga a robotelului cu 90 de grade?

O intoarcere la stanga cu 90 de grade inseamna de fapt ca vrem sa rotim vectorul de directie (dx, dy) cu 90 de grade (adica pi/2 radiani) in sens trigonometric. Adica, altfel spus, asta inseamna sa adunam pi/2 la unghiul vectorului (dx, dy) vazut ca numar complex.

Hooopaa! Asta suna ca rezultatul unui produs de numere complexe (cum am discutat mai devreme), nu? Trebuie doar sa avem grija ca modulul lui (dx, dy) sa ramana nemodificat. Adica modulul numarului complex cu care il vom inmulti pe dx+i*dy trebuie sa fie 1. Iar unghiul acelui numar trebuie sa fie pi/2 radiani.

In concluzie, din discutia asta rezulta ca daca vreau sa rotesc cu 90 de grade la stanga directia de mers a robotelului (adica versorul (dx, dy)) trebuie sa inmultesc numarul complex dx+i*dy cu numarul complex 1*e^(i*pi/2) = cos(pi/2) + i*sin(pi/2) = i.

Si daca fac calculul (dx+i*dy)  inmultit cu i obtin dx*i + i*dy*i, ceea ce este egal cu i*dx – 1*dy. Obtin, adica, numarul complex -dy+i*dx.

Deci varianta rotita la stanga cu 90 de grade a vectorului (dx, dy) este vectorul (-dy, dx). Voila! 🙂

Similar se face calculul si pentru a obtine rotatia la dreapta. (Daca ai inteles explicatia, imi poti spune cu ce numar complex trebuie sa-l inmultesc pe dx+i*dy pentru a obtine varianta rotita cu 90 de grade la dreapta a vectorului (dx, dy)?)

Ai vazut, deci, cum poti roti un robotel folosind numere complexe. Sa mai zica cineva ca numerele complexe nu sunt cool! 🙂

Cu drag,

Florin