Lectia de azi e una speciala, caci vei invata sa faci singur un joc. Un joc intreg, de la cap la coada, pornind de la zero. (Bine, nu chiar de la zero, ci de la lectiile anterioare de introducere in programare, lectii in care te-am luat de la zero si te-am adus pas cu pas pana in punctul in care esti in stare sa-ti programezi propriul joc.)

Vei vedea in lectia de azi pas cu pas cum am gandit jocul si cum l-am realizat.

In esenta sunt necesari doar doi pasi si trei miscari. Serios. 🙂

Voi detalia toate aceste etape pe un joc pe care il vom aduce impreuna de la stadiul de idee la stadiul de realizare practica. Este vorba de un joc de labirint, in care scopul va fi sa deplasezi (cu ajutorul unor taste) un omulet printr-un spatiu cu trasee libere si pereti pana la o anumita destinatie.

Am zis ca pentru a realiza acest joc e nevoie de doar doi pasi si trei miscari. Si am vorbit serios. Hai sa vedem care ar fi acestia.

In primul rand, cei doi pasi.

Pasul 1 — proiectarea

Primul pas in realizarea unui joc este proiectarea lui. Nu are sens sa te apuci direct de partea de implementare atata timp cat nu stii foarte clar ce vrei sa obtii si cum anume.

Imaginea aceea de programator care se aseaza la calculator si se apuca direct sa programeze e doar de spectacol.

Toti programatorii (buni) isi fac mai inainte un plan. (Chiar daca, poate, in unele cazuri acest plan este facut doar mental si cu o viteza atat de mare incat pare ca omul acela scrie direct programul fara sa-l fi gandit in prealabil.)

In cadrul acestui prim pas (care este extrem de important) voi detalia ulterior cele trei miscari esentiale pentru realizarea lui.

Pasul 2 — programarea

Abia dupa ce ai dedicat programului o buna cantitate de gandire si ai indeplinit cu succes cele trei miscari din cadrul pasului de proiectare e cazul sa te apuci de programarea propriu-zisa.

In functie de cat de bine ai indeplinit primul pas (pasul de proiectare), pasul al doilea (pasul de programare) va fi mai mult sau mai putin o formalitate. Scrierea unui program bine gandit in prealabil este o sarcina foarte usoara.

Nu este exclus, insa, nici ca in cadrul acestei etape sa iasa la iveala unele lucruri care au scapat in faza de proiect, caz in care va trebui sa revii la pasul anterior si sa regandesti programul tinand cont de noile date dobandite.

Prin urmare, pasul de proiectare este unul de o importanta covarsitoare in realizarea unui program de calculator (in general, si a unui joc, in particular). El te va urma intr-o forma sau alta pe toata perioada realizarii jocului.

Asa ca haide sa detaliem pasul de proiectare a jocului si sa vedem care sunt cele trei miscari necesare pentru realizarea lui. Le voi si exemplifica practic pe jocul nostru de labirint.

Miscarea 1 — specificatiile

Bun, vreau sa fac un joc. De unde incep?

In primul rand trebuie sa stabilesc cat mai clar cu putinta ce vreau sa fac. Mai exact, trebuie sa definesc interfata grafica si comportamentul programului.

Asa ca primul lucru pe care il fac atunci cand ma apuc sa construiesc un joc este sa ii desenez pe o foaie interfata, adica modul cum vreau sa arate el pe ecran.

De asemenea, pe langa aceasta interfata trebuie sa specific comportamentul, si in special modul cum vreau ca interfata grafica sa raspunda la comenzile utilizatorului (adica la apasarea unor taste).

In cazul jocului nostru de labirint interfata dorita este cea din imaginea alaturata. In aceasta imagine punctul verde este omuletul (sau marioneta pe care o vom plimba prin labirint), punctele albe sunt traseele libere pe care omuletul se poate deplasa, punctele negre sunt peretii labirintului, iar punctul rosu este destinatia unde omuletul trebuie sa ajunga.

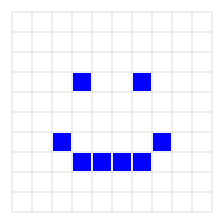
Cat priveste comportamentul programului, acesta este urmatorul. La pornirea jocului se va desena interfata grafica, adica se vor desena peretii si se vor plasa omuletul si destinatia asa cum am aratat in imagine. Apoi, la fiecare apasare a vreuneia din tastele 'a' (stanga), 's' (jos), 'd' (dreapta) sau 'w' (sus) omuletul se va deplasa cu o pozitie in directia indicata. Deplasarea aceasta se va face doar daca in directia respectiva nu este perete sau marginea ecranului nostru de 10×10 puncte. In momentul in care omuletul ajunge la destinatie jocul se va incheia (adica programul nu va mai raspunde la apasarea tastelor, ecranul se va sterge si se va afisa un zambet albastru (si anume cel pe care l-ai vazut reprezentat in prima imagine din acest articol)).

Miscarea 2 — datele

Odata ce am realizat miscarea anterioara (deci odata ce stiu cum vreau ca jocul sa arate si sa se comporte), urmatoarea etapa in realizarea lui consta in a stabili ce variabile imi trebuiesc in spatele lui.

Cu alte cuvinte, trebuie sa analizez rezultatele etapei anterioare si sa decid ce elemente din interfata si din comportamentul programului necesita memorarea unor date (care eventual trebuie sa poata fi modificate pe parcursul derularii jocului).

Aceasta este o etapa foarte importanta (si pe care cel mai probabil va trebui sa o antrenezi o vreme pentru a ajunge sa o realizezi cu usurinta), caci in cadrul acestei etape practic abstractizezi jocul. Pornesti de la concret, de la cum vrei sa arate si sa se comporte jocul, si ajungi sa scoti din el niste numere (fixe (constante) sau variabile) care ii modeleaza complet atat felul cum arata pe ecran, cat si modul in care se comporta.

Daca miscarea anterioara a presupus desene si text, in cadrul miscarii curente cuvantul cheie este numarul. (Pitagora spunea ca orice lucru poate fi redus la un numar. Daca te uiti la muzica ta (siruri de numere in format MP3) sau la cartile tale (siruri de numere in format PDF) cu siguranta vei fi tentat sa ii dai dreptate. Daca te vei uita, insa, la inteligenta si la procesele complexe ce se produc in creierul tau vei realiza ca dezbaterea asta e departe de a fi incheiata.)

Practic, pentru ca un joc sa poata fi realizat pe calculator trebuie sa indeplineasca conditia de a putea fi modelat in intregime cu ajutorul numerelor. Iar etapa curenta are rolul de a obtine tocmai acest model pe baza de numere al jocului.

Hai sa vedem concret prin ce numere am putea sa modelam jocul nostru de labirint.

Avem in joc un omulet care pe parcursul jocului se poate gasi in diverse pozitii din labirint. Prin urmare, trebuie sa avem niste variabile in care sa ii memoram pozitia curenta. Sa denumim aceste variabile ox si oy. Asadar, (ox, oy) vor reprezenta coordonatele omuletului pe ecranul de 10×10 puncte.

De asemenea, avem in labirint o pozitie speciala — destinatia unde trebuie sa ajunga omuletul. O putem memora in alte doua variabile, dx si dy. (De remarcat aici faptul ca aceasta destinatie nu se schimba pe parcursul jocului (asa ca dx si dy vor fi utilizate pe post de constante (si nu de variabile, asa cum le zice numele)).)

In plus, peretii si traseele au o configuratie speciala, si anume cea aratata in figura de la etapa anterioara. Este necesar sa avem un mijloc de a putea spune daca un anumit punct de pe ecran este traseu liber sau este perete al labirintului. Putem face asta cel mai facil cu ajutorul unei matrici. In aceasta matrice (sa o denumim, de exemplu, mp (de la matricea peretilor)) va trebui sa avem elemente pentru fiecare punct de pe ecran si in fiecare astfel de element in parte vom putea memora valoarea 1 pentru elementele ce corespund unor puncte unde se gasesc pereti, si valoarea 0 pentru elemente ce corespund unor puncte unde se gaseste traseu liber.

In mod normal ar fi suficienta in acest sens o matrice, mp, de 10 linii si 10 coloane. Cum, insa, numerotarea liniilor si a coloanelor incepe nu de la 1, ci de la 0, am ales sa folosesc (pentru sporirea claritatii programului rezultat) o matrice de 11×11 in care prima linie (linia cu indicele 0) si prima coloana (coloana 0) le voi lasa neutilizate. (Da, voi face risipa de memorie in scop didactic 🙂 .)

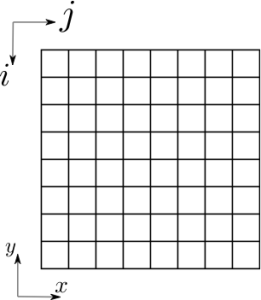
OK, deci am o matrice mp in care elementul mp[i][j] este 1 pentru perete si 0 pentru traseu liber. Dar i si j de aici sunt indici de linie si respectiv de coloana, si nu coordonate pe ecran. Reamintesc faptul ca originea sistemului de coordonate ale punctelor de pe ecran este in coltul stanga jos (cu x crescand de la 1 cu cate o unitate spre dreapta, si cu y crescand de la 1 cu cate o unitate in sus), iar originea indicilor de linie si de coloana pentru o matrice este in coltul din stanga sus (cu indicele de linie (i) crescand cu cate o unitate in jos, si cu indicele de coloana (j) crescand cu cate o unitate la dreapta).

Prin urmare, in cadrul programului va trebui sa pot face usor translatarea de la coordonatele de pe ecran la coordonatele din matrice. De exemplu, punctului (1, 1) de pe ecran ii corespunde elementul [10][1] din matrice (in conditiile in care, asa cum am spus, linia 0 si coloana 0 din matrice le las neutilizate). Similar, elementul [2][9] din matrice corespunde punctului (9, 9) de pe ecran.

Cum pot face translatarea aceasta? Pentru coordonata de pe axa x e simplu, caci aceasta practic va coincide cu indicele de coloana din matricea mp. Pentru coordonata de pe axa y este un pic mai dificil, caci y variaza de jos in sus, in vreme ce indicele de linie, i, variaza de sus in jos. Acest sens de variatie diferit imi spune ca in expresia lui i y va aparea cu semnul minus (si, de asemenea, in expresia lui y i va aparea cu semnul minus).

Hai sa pornim de la punctul (1, 1) de pe ecran. Pentru acest punct, y = 1. Lui ii corespunde din matricea mp elementul [10][1]. Deci i = 10.

Mai intai vreau sa obtin expresia lui y in functie de i. Stiu pana aici doar ca in aceasta expresie apare termenul -i. Adica pana aici am doar y = -i… . Adica 1 = -10… . Este clar, deci, cum trebuie sa completez expresia pentru a avea egalitate. 1 = -10+11. Adica y = 11-i. Expresia se verifica pentru toate punctele de la (1, 1) la (1, 10).

Pot obtine expresia lui i in functie de y rearanjand expresia anterioara. Rezultatul va fi i = 11-y.

Asadar, daca vreau sa aprind pe ecran punctul ce corespunde elementului mp[i][j], voi aprinde punctul (j, 11-i). Iar daca vreau sa verific daca e perete in punctul (x, y), voi testa valoarea elementului mp[11-y][x].

In plus fata de variabilele discutate pana aici vom avea nevoie si de niste variabile pe care sa le folosim pe post de indici cu care sa parcurgem matricea mp. Aceste variabile nu fac parte efectiv din modelul jocului, ci sunt variabile auxiliare, ce ne sunt necesare ca instrumente in implementare. Le voi denumi l (de la linie) si c (de la coloana). (Ele vor corespunde lui i si j din discutia anterioara.)

Miscarea 3 — schita

Odata ajunsi in punctul asta, suntem gata sa incepem schitarea programului. Scopul nu este sa obtinem direct codul sursa pe care il vom scrie in simulator, ci o schita generala, care sa ne arate intr-un limbaj natural ce va contine programul.

Pentru jocul nostru de labirint schita aceasta ar putea fi urmatoarea:

• -> Definire variabile (ox, oy, dx, dy, mp, l, c)
• -> Initializari (definire trasee si pereti (mp), pozitie destinatie (dx, dy), pozitie omulet (ox, oy))
• -> Desenare interfata (desenare pereti, desenare destinatie, desenare omulet)
• -> Definire functie taste

Daca la primele trei puncte din aceasta schita cred ca este destul de clar ce e de facut, ultimul dintre ele necesita detaliere. Asta voi face in continuare.

-> Definire functie taste:

• –> daca s-a apasat vreo tasta de directie, atunci incearca deplasarea in directia aia (folosind doua noi variabile auxiliare locale, oxnou si oynou, si avand grija sa nu se iasa in afara ecranului)
• –> daca la noua pozitie nu e perete, atunci deplaseaza omuletul acolo
• –> daca omuletul e la destinatie, atunci incheie jocul si afiseaza zambet albastru

Gata! Abia dupa ce am ajuns in punctul asta e cazul sa ne punem problema scrierii codului sursa al programului. Ce urmeaza nu este chiar departe de a fi o simpla formalitate odata ce ajungi sa stapanesti bine fundamentele programarii. Dificultatea semnificativa in constuirea unui joc o constituie indeplinirea cu succes a acestor trei miscari pe care le-am discutat aici.

Mai jos voi prezenta programul pentru jocul de labirint, asa cum a rezultat in urma etapelor exemplificate in acest articol. Ti-as recomanda ca inainte de a-l citi sa iti scrii tu propriul program si doar atunci cand intampini dificultati sa te inspiri din exemplul meu. In multe locuri din acest program puteam sa fac lucrurile in alt mod (si uneori chiar mai eficient decat am facut-o). Asa ca te-as ruga sa nu citesti programul de mai jos cu evlavia datorata unui text sfant, ci sa-l folosesti doar ca termen de comparatie pentru programul tau :-). Nu va fi un exercitiu usor pentru tine, dar rezultatele vor fi spectaculoase si iti vei multumi ca ai facut-o.

// ——————–
// | Joc de labirint |
// ——————–

// –> Definire variabile:

// omuletul
var ox
var oy

// destinatia
var dx
var dy

// traseul si peretii
var mp = Matrice(11, 11)

// variabile ajutatoare
var l
var c

// –> Initializari:

// omuletul
ox = 1
oy = 1

// destinatia
dx = 10
dy = 10

// traseul si peretii
l = 1
while (l<=10)
{
  c = 1
  while (c<=10)
  {
    mp[l][c] = 0
    c = c+1
  }
  l = l+1
}
mp[1][1]=1; mp[2][1]=1; mp[3][1]=1; mp[4][1]=1;
mp[5][1]=1; mp[6][1]=1; mp[7][1]=1; mp[8][1]=1;
mp[9][1]=1; mp[2][2]=1; mp[6][2]=1; mp[9][2]=1;
mp[2][3]=1; mp[4][3]=1; mp[6][3]=1; mp[8][3]=1;
mp[9][3]=1; mp[4][4]=1; mp[8][4]=1; mp[9][2]=1;
mp[2][5]=1; mp[3][5]=1; mp[4][5]=1; mp[5][5]=1;
mp[6][5]=1; mp[8][5]=1; mp[10][5]=1; mp[2][6]=1;
mp[4][6]=1; mp[8][6]=1; mp[2][7]=1; mp[4][7]=1;
mp[5][7]=1; mp[6][7]=1; mp[8][7]=1; mp[9][7]=1;
mp[2][8]=1; mp[9][8]=1; mp[2][9]=1; mp[4][9]=1;
mp[5][9]=1; mp[6][9]=1; mp[7][9]=1; mp[8][9]=1;
mp[9][9]=1; mp[2][10]=1;

// –> Desenare interfata:

// desenare pereti
l = 1
while (l<=10)
{
  c = 1
  while (c <= 10)
  {
    if (mp[l][c] == 0)
    {
      Stinge(c, 11-l)
    }
    else
    {
      Aprinde(c, 11-l, NEGRU)
    }
    c = c+1
  }
  l = l+1
}

// desenare destinatie
Aprinde(dx, dy, ROSU)

// desenare omulet
Aprinde(ox, oy, VERDE)

// –> Definire functie taste:

function FunctieTaste(ev)
{
  var tasta = TastaApasata(ev)
  // daca s-a apasat vreo tasta de directie,
  // atunci incearca deplasarea in directia aia
  var oxnou = ox
  var oynou = oy
  if ( (tasta == 'a') && (ox > 1) )
  {
    oxnou = ox-1
  }
  if ( (tasta == 'd') && (ox < 10) )
  {
    oxnou = ox+1
  }
  if ( (tasta == 's') && (oy > 1) )
  {
    oynou = oy-1
  }
  if ( (tasta == 'w') && (oy < 10) )
  {
    oynou = oy+1
  }
  Stinge(ox, oy)
  // daca la noua pozitie nu e perete,
  // atunci deplaseaza omuletul acolo
  if (mp[11-oynou][oxnou] != 1)
  {
    ox = oxnou
    oy = oynou
  }
  Aprinde(ox, oy, VERDE)
  // daca omuletul e la destinatie,
  // atunci incheie jocul si afiseaza zambet
  if ( (ox == dx) && (oy == dy) )
  {
    //inceteaza ascultarea tastelor
    AscultaTaste()
    // sterge ecranul
    l = 1
    while (l <= 10)
    {
      c = 1
      while (c <= 10)
      {
        Stinge(c, 11-l)
        c = c+1
      }
      l = l+1
    }
    // afiseaza zambet
    Aprinde(3, 4, ALBASTRU)
    Aprinde(4, 3, ALBASTRU)
    Aprinde(5, 3, ALBASTRU)
    Aprinde(6, 3, ALBASTRU)
    Aprinde(7, 3, ALBASTRU)
    Aprinde(8, 4, ALBASTRU)
    Aprinde(4, 7, ALBASTRU)
    Aprinde(7, 7, ALBASTRU)
  }
}

AscultaTaste(FunctieTaste)

Iata si simulatorul nostru de zbor pe taramul creativitatii. Astazi vei vedea cu ochii tai cum programul prinde aripi si dintr-o insiruire de comenzi ca cele invatate in lectiile trecute devine un joc serios care te pune la munca sa iti scoti omuletul verde din temnita intortocheata in care a fost aruncat.

Iti urez distractie placuta in construirea si jucarea acestui joc de labirint.

Si te rog sa imi spui intr-un comentariu mai jos care activitate ti se pare mai facila: gasirea drumului intr-un labirint, sau programarea unui joc de labirint? (Astept cu drag raspunsurile tale 🙂 .)

Florin Bîrleanu