Programarea nu exista fara date. Cu toate ca instructiunile sunt cele care sar in ochi atunci cand te gandesti la un program de calculator, datele sunt esenta.

Datele sunt “sufletul” programului. Restul programului, algoritmul, e doar o secventa de pasi menita sa opereze asupra acelor date.

Iar operarea asta poate sa fie mai facila sau mai complicata, mai rapida sau mai lenta, mai clara sau mai obscura, in functie de modul cum sunt organizate acele date.

Am vorbit in Abecedarul de programare despre structurile de date fundamentale si sper ca te-ai “jucat” un pic cu ele pentru a intelege cum functioneaza.

Iata aici un mic “reminder”:

Acum o sa vorbim despre cum poti programa in C aceste structuri de date.

Lista

Lista (=”list”, in engleza) este o colectie liniara de elemente. Adica exista o ordine a elementelor in acea lista — exista un prim element, un al doilea element, … si un ultim element.

Auzind asta, probabil ca te gandesti imediat la un vector.

E adevarat ca si vectorul e o colectie liniara de elemente, dar lista e mai mult de atat. Vectorul e doar o varianta concreta de implementare a unei liste (asa cum vom vedea in continuare), insa lista e un tip de date abstract ce trebuie sa permita urmatoarele operatii:

• adaugare element la finalul listei: Add(lista, element)
• accesare valoare element de pe o pozitie specificata din lista: Get(lista, pozitie)
• inserare element intr-o pozitie specificata in lista: Insert(lista, element, pozitie)
• stergere element de pe o pozitie specificata din lista: Delete(lista, pozitie)

Si e util sa avem si posibilitatea de a afla numarul curent de elemente din lista, adica sa aflam lungimea listei: Length(lista). (Sau, altfel, poti parcurge lista element cu element pana cand functia Get iti returneaza un cod care sa iti indice faptul ca nu exista element pe acea pozitie. Numarul primei pozitii care nu contine element este dimensiunea listei.)

Evident, daca Length(lista) == 0 inseamna ca lista e goala (vida).

Concret, o lista poate fi implementata in mai multe moduri, cum ar fi:

1. printr-un vector (si o variabila in care sa memoram numarul de elemente din lista)
2. prin inregistrari (struct) inlantuite cu ajutorul pointerilor.

Ar fi multe de luat in calcul pentru a alege varianta cea mai buna de implementare a unei liste pentru o aplicatie anume. (Si cand zic “cea mai buna” ma refer la “cea mai rapida” si “care sa utilizeze cat mai putina memorie”.)

Foarte simplist vorbind, implementarea pe baza de vector ar fi o solutie acceptabila atunci cand dimensiunea maxima pe care o poate avea lista e cunoscuta in avans si nu e foarte mare.

In caz contrar, va trebui sa o implementezi ca lista inlantuita. Iar aici ai doua variante: simplu inlantuita (in care fiecare element contine (pe langa valoare) si o legatura (un pointer) catre elementul urmator) sau dublu inlantuita (in care fiecare element contine legaturi atat catre elementul urmator din lista, cat si catre elementul anterior).

Ce varianta alegi intre simplu inlantuita si dublu inlantuita?

E alegerea ta. Trebuie sa te gandesti ca varianta a doua permite parcurgerea mai facila (mai rapida) a listei in ambele sensuri, dar ocupa mai multa memorie (pentru ca fiecare element va contine, pe langa valoare, doi pointeri (in loc de unul singur)).

Fiecare element din cadrul unei liste inlantuite e o inregistrare (un struct din C) ce contine o valoare (sau mai multe valori, de oricare dintre tipurile primare de date) si unul sau doi pointeri. Elementul va fi construit in memorie abia in momentul in care avem nevoie de el si putem elibera memoria respectiva cand nu mai avem nevoie de el (asa cum am vorbit la lectia despre alocarea dinamica a memoriei in C).

Stiva

Stiva (=”stack”, in engleza) e un tip de date abstract ce trebuie sa permita doua operatii:

• adaugare element in varful stivei: Push(stiva, element)
• extragere element din varful stivei: Pop(stiva).

Si mai trebuie sa avem posibilitatea de a afla cand stiva e goala. (Dar poti face asta prin a face ca functia Pop sa iti returneze un anumit cod care sa iti indice faptul ca stiva e goala. Sau poti implementa o functie de genul StackEmpty(stiva) care sa iti returneze 1 daca stiva e goala si 0 daca nu.)

Deci si stiva e o structura de date liniara, ca si lista. Am putea zice ca stiva e un fel de lista care permite doar adaugarea si extragerea de elemente pe la un acelasi capat al listei. Iar acel capat se numeste varful stivei.

Asta inseamna ca ultimul element introdus in stiva va fi primul element pe care il vei putea scoate din ea. (In engleza asta se zice prin acronimul LIFO (last in, first out — ultimul intrat, primul iesit).)

Am zis ca stiva e un tip de date abstract (ca si lista, de fapt), adica nu e dependenta de un anumit mod de stocare a datelor in memorie. Atata timp cat cele doua operatii de care am vorbit sunt disponibile, stiva poate fi implementata practic in mai multe moduri, cum ar fi:

1. printr-un vector (si o variabila in care memoram indexul varfului stivei)
2. printr-o lista simplu inlantuita.

Coada

Coada (=”queue”, in engleza) este o structura de date “inrudita” cu stiva. E tot liniara si permite tot doua operatii (adaugare de element si extragere de element), doar ca:

• adaugarea de element se face doar pe la un capat al cozii (capat numit coada (“tail”, in engleza))
• extragerea de element se face doar pe la un capat al cozii (capat numit cap (“head”, in engleza)).

Asta inseamna ca primul element introdus in stiva va fi primul element pe care il vei putea scoate din ea. (In engleza asta se zice prin acronimul FIFO (first in, first out — primul intrat, primul iesit).)

Coada poate fi implementata concret in mai multe moduri, cum ar fi:

1. printr-un vector circular (cum am aratat si in Abecedar)
2. printr-o lista dublu inlantuita, cu doua “santinele” (si anume, pointerii pentru coada si capul listei).

Arbore

Arborele (=”tree”, in engleza) e o structura de date ierarhica formata din noduri ce au legaturi intre ele. Pana aici, definita asta e valabila pentru o structura de date mai generica decat arborele — graful orientat.

Matematic vorbind, arborele ar fi un graf orientat conex si fara cicluri si in care avem un prim nod (pe care il numim radacina arborelui) si exista pentru fiecare nod cate un drum ce pleaca din radacina si ajunge la acel nod. Nodurile terminale se numesc frunze.

Practic, intr-un arbore avem asa:

• un nod de unde incepe arborele (nodul-radacina)
• radacina va contine legaturi catre alte noduri (numite noduri-fii (“child nodes”) pentru nodul-radacina), iar pentru acele noduri radacina va fi nod-parinte (“parent node”)
• fiecare fiu al radacinii poate avea, la randul lui, proprii fii
• si asa mai departe, pana cand ajungem (pe toate “ramurile” arborelui (care arata mai degraba a arbust, intre noi fie vorba)) la noduri ce nu mai au fii
• aceste noduri (care nu mai au fii) se numesc frunze (“leaf nodes”).

Uite o “poza” cu un arbore:

/
     bin
     home
         florinb
     usr
         bin
         lib

E vorba de o parte dintre dosarele de pe calculatorul meu. Le pot reprezenta ca o lista ordonata asa (specificand pentru fiecare dintre dosare calea completa):

1. /
2. /bin
3. /home
4. /home/florinb
5. /usr
6. /usr/bin
7. /usr/lib

Vazute ca arbore, ar fi asa:

• nodul 1 e radacina si are 3 fii: nodurile 2, 3 si 5
• nodul 3 are 1 fiu: nodul 4
• nodul 5 are 2 fii: nodurile 6 si 7

Cum se poate implementa un arbore?

Evident, raspunsul e ca un arbore se poate implementa in mai multe moduri (alegerea intre ele putandu-se face in functie de aplicatie, tinand seama de mai multe criterii (cum ar fi: dificultatea de implementare, cantitatea de memorie ocupata si viteza de rulare)).

Cel mai natural, insa, ar fi sa facem o inregistrare (struct) ce va contine:

• informatia din acel nod (adica datele utile stocate in acel nod)
• si o lista de legaturi catre fiii nodului.

Arbore binar de cautare

Arborii au extrem de multe aplicatii practice. Hai sa vorbim putin despre una dintre ele.

Gandeste-te cat ar dura sa cauti intr-o lista un element cu o anumita valoare.

Evident, depinde de viteza calculatorului respectiv — dar nu la asta ma refer prin “cat ar dura”, ci ma refer la “cate operatii” ar trebui sa efectueze programul tau pentru a cauta daca in lista exista sau nu vreun element cu valoarea cautata.

Daca lista are N elemente, in cel mai rau caz ar “dura” N operatii (de prelucrare element din lista si de comparare a (valorii) lui cu valoarea cautata).

De exemplu, daca am avea urmatoarea lista de numere:

[12, 1, 3, 7, 4, 2, 6, 10, 8, 9, 5, 15, 13, 14, 11]

si am vrea sa cautam daca exista in ea vreun element cu valoarea 11, ar trebui sa ne uitam pe rand la fiecare element. (Daca il gasim, terminam cautarea acolo; daca nu, trebuie sa parcurgem lista pana la final.)

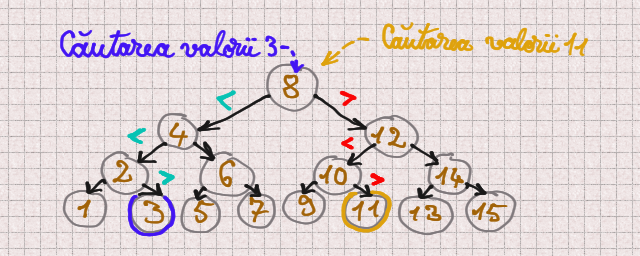
Dar daca am avea aceleasi numere organizate intr-un arbore binar (adica un arbore in care fiecare nod (cu exceptia frunzelor) are cate doi fii) si daca am sti despre acest arbore ca a fost construit astfel incat pentru fiecare nod subarborele sau din stanga sa contina doar valori mai mici decat valoarea din acel nod (iar subarborele din dreapta sa contina doar valori mai mari decat valoarea din acel nod)?…

Arborele asta ar putea arata asa:

Cate operatii ar “dura” cautarea unei valori intr-un astfel de arbore?

Maxim 4 operatii (adica log2(16)). (Iar acest maxim s-ar atinge doar in cazul in care valoarea cautata nu exista in arbore.)
E mult mai bine decat maxim 15 operatii, nu-i asa? 🙂

Dictionar

Pe o structura de date similara cu arborele binar de cautare am putea implementa si un “dictionar” care sa ne ajute sa cautam rapid “explicatia” unui “cuvant” oarecare dintr-o multime de cateva mii de cuvinte.

Gandeste-te ca daca ai avea 1000 de cuvinte in dictionar nu ar trebui sa faci zeci, sute (sau chiar 1000, in cel mai rau caz) de cautari. Ci ar fi suficiente maxim 10 (=log2(1024)) cautari.

In cazul structurii de date numita dictionar in programare “cuvantul” se numeste cheie (=”key”, in engleza), iar “explicatia” se numeste valoare (=”value”, in engleza). Iar dictionarul este o colectie de perechi (cheie, valoare).

Si, bineinteles, e implementat intr-un mod care sa permita cautarea rapida a oricarei chei din dictionar.

Implementarea inregistrarilor inlantuite

Pentru a implementa in C structurile de date de care am vorbit, cea mai flexibila metoda e sa te folosesti de inregistrari inlantuite alocate dinamic in memorie.

In acest video live poti vedea cum am facut practic asta pentru a implementa in C o lista si o stiva folosind alocarea dinamica a memoriei:

Stiu ca nu e chiar usor (ba chiar e destul de dificil, ai dreptate), dar daca ti-ai construit o fundatie solida in materie de programare (de exemplu, studiind Abecedarul de programare) si apoi ai urmat cu rabdare fiecare din pasii acestui tutorial de C, atunci cred ca aceasta lectie ti-a sporit interesul pentru programare si ti-a intarit si mai mult curiozitatea de a afla mai multe despre acest domeniu fascinant.

 

 

Cu drag,

Florin Bîrleanu